初中数学重点：【一元二次方程】知识点汇总！

一元二次方程作为初中阶段重点难点，更是全国中考的高频考点，在选择、填空和解答题均有所涉及。今天老师就来说说一元二次方程的基本知识点，赶快来看看吧！

一、一元二次方程的有关概念

1. 一元二次方程的概念：

通过化简后，只含有一个未知数(一元)，并且未知数的*高次数是2(二次)的整式方程，叫做一元二次方程。

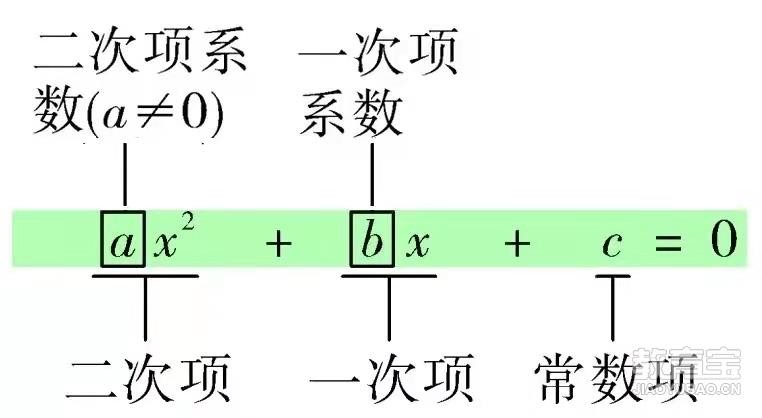
2. 一元二次方程的一般式：

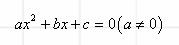
3.一元二次方程的解：

使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解，也叫做一元二次方程的根。

细节剖析

判断一个方程是否为一元二次方程时，首先观察其是否是整式方程，否则一定不是一元二次方程；其次再将整式方程整理化简使方程的右边为0，看是否具备另两个条件：

①一个未知数；②未知数的*高次数为2。

对有关一元二次方程定义的题目，要充分考虑定义的三个特点，不要忽视二次项系数不为0。

二、一元二次方程的解法

1．基本思想：

2．基本解法：

直接开平方法、因式分解法、公式法、配方法。

【温馨提示】解一元二次方程时一般不使用配方法（除特别要求外），但必须熟练掌握.解一元二次方程选择方法的一般顺序是：直接开平方法→因式分解法→公式法→配方法。

三、一元二次方程根的判别式及根与系数的关系

1. 一元二次方程根的判别式 ：

①当△>0时，一元二次方程有2个不相等的实数根；

②当△=0时，一元二次方程有2个相等的实数根；

③当△<0时，一元二次方程没有实数根。

2. 一元二次方程的根与系数的关系：

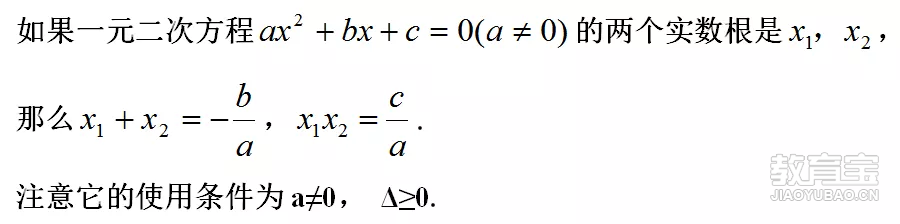
细节剖析

1. 一元二次方程根的判别式正反都成立。利用其可以解决以下问题：

①不解方程判定方程根的情况；

②根据参系数的性质确定根的范围；

③解与根有关的证明题．

2. 一元二次方程根与系数的应用很多：

①已知方程的一根，不解方程求另一根及参数系数；

②已知方程，求含有两根对称式的代数式的值及有关未知数系数；

③已知方程两根，求作以方程两根或其代数式为根的一元二次方程。

四、列一元二次方程解应用题

1. 列方程解实际问题的三个重要环节：

　一是整体地、系统地审题；

　二是把握问题中的等量关系；

　三是正确求解方程并检验解的合理性.

2. 利用方程解决实际问题的关键是寻找等量关系.

3. 解决应用题的一般步骤：

审：审题目、分清已知量、未知量、等量关系等；

设：设未知数，有时会用未知数表示相关的量；

列：根据题目中的等量关系，列出方程；

解：解方程，一元二次方程应用题一般能用因式分解法；

验：检验方程的解能否保证实际问题有意义；

答：写出答案，切忌答非所问；

4. 常见应用题型：

数字问题、平均变化率问题、利息问题、利润(销售)问题、形积问题等.

细节剖析

列方程解应用题就是先把实际问题抽象为数学问题（列方程），然后由数学问题的解决而获得对实际问题的解决.